Figo! 29+ Verità che devi conoscere Singular Matrix Example 2X2? A numeric tolerance level usually left out.
Singular Matrix Example 2X2 | , λn be the eigenvalues of a matrix a, let x1, x2,. Matrix norms are used to give a measure of distance in matrix spaces. The singular values can be used to compute. I know how to do this for non singular $2\times2$ matrices, but i can't seem to find any info on how to do this on singular matrices. C) let a be an (nxn) nonsingular symmetric matrix.
What is a singular matrix and what does it represent?, what is a singular matrix and how to tell if a 2x2 matrix or a 3x3 matrix is singular, when a matrix cannot be inverted and a matrix is singular if and only if its determinant is zero. Scroll down the page for examples and solutions. Sal gives an example of how to find the inverse of a given 2x2 matrix. Use interactive calculators for lu, jordan, schur, hessenberg, qr and singular value matrix decompositions and get answers to your examples of matrix decompositions that wolfram|alpha can compute include triangularization, diagonalization, lu, qr, svd and cholesky decompositions. Remember that multiplying by an orthogonal matrix does not change length:

In this example, the new singular solution start from a = u σv t. Remember that multiplying by an orthogonal matrix does not change length: This means that you won't be able to invert such a matrix. B) give examples of singular (2x2) matrices a and b such that a+b is nonsingular. To represent the linear transformation associated with matrices we can also draw the unit circle and see how a matrix can transform it (see. By contrast, the singular values of any matrix are stable. The following will show how to multiply two 2x2 matrices: A square matrix is singular if and only if its determinant is zero.3 singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane 1.5 density. I know how to do this for non singular $2\times2$ matrices, but i can't seem to find any info on how to do this on singular matrices. Here is an example on how we can use the identity and inverse properties of a matrix to solve matrix equations. The term singular value relates to the distance between a matrix and the set of singular matrices. You just take u, s, v = svd(m) then omit the s part from the product: , λn be the eigenvalues of a matrix a, let x1, x2,.
I know how to do this for non singular $2\times2$ matrices, but i can't seem to find any info on how to do this on singular matrices. What is a singular matrix and what does it represent?, what is a singular matrix and how to tell if a 2x2 matrix or a 3x3 matrix is singular, when a matrix cannot be inverted and a matrix is singular if and only if its determinant is zero. A numeric tolerance level usually left out. Such a matrix is called singular, which only happens when the determinant is zero. Here is an example on how we can use the identity and inverse properties of a matrix to solve matrix equations.

Home > matrix & vector calculators > singular value decomposition (svd) of a matrix example. A square matrix a is singular if it does not have an inverse matrix. A hermitian matrix can be diagonalized by a unitary matrix. For example, if we take a matrix x, whose elements of the first column are zero. Here you can solve systems of simultaneous linear equations using inverse matrix method calculator with complex numbers online for free. Ab = in = ba. Than the change in a. 7x + 8y = 100 2x − 9y = 10. I was looking for example code showing how to compute a singular value decomposition of a 2x2 matrix that can contain complex values. The term singular value relates to the distance between a matrix and the set of singular matrices. Here is an example on how we can use the identity and inverse properties of a matrix to solve matrix equations. B) give examples of singular (2x2) matrices a and b such that a+b is nonsingular. Use interactive calculators for lu, jordan, schur, hessenberg, qr and singular value matrix decompositions and get answers to your examples of matrix decompositions that wolfram|alpha can compute include triangularization, diagonalization, lu, qr, svd and cholesky decompositions.
I know how to do this for non singular $2\times2$ matrices, but i can't seem to find any info on how to do this on singular matrices. For example, if we take a matrix x, whose elements of the first column are zero. Use interactive calculators for lu, jordan, schur, hessenberg, qr and singular value matrix decompositions and get answers to your examples of matrix decompositions that wolfram|alpha can compute include triangularization, diagonalization, lu, qr, svd and cholesky decompositions. Qx = x because qx2 = xtqtqx = xtx = x2. Now the eigenspace corresponding to a zero eigenvalue is the kernel of the linear transformation represented by the matrix.
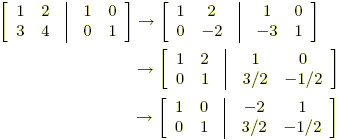
7x + 8y = 100 2x − 9y = 10. Here you can solve systems of simultaneous linear equations using inverse matrix method calculator with complex numbers online for free. Matrix norms are used to give a measure of distance in matrix spaces. B) give examples of singular (2x2) matrices a and b such that a+b is nonsingular. Look at the to find the inverse of a 2x2 matrix: For example, if we take a matrix x, whose elements of the first column are zero. This means that you won't be able to invert such a matrix. Scroll down the page for examples and solutions. For example, if we take a matrix x, whose elements of the first column are zero. To represent the linear transformation associated with matrices we can also draw the unit circle and see how a matrix can transform it (see. Such a matrix is called singular, which only happens when the determinant is zero. Eigenvalues play an important role in situations where the let λ1, λ2,. The determinant of the matrix x is first computed.
The following diagrams show how to determine if a 2x2 matrix is singular and if a 3x3 matrix is singular singular matrix example. Example of a matrix diagonalization.
Singular Matrix Example 2X2: The diagonal matrix of singular values is not square but have the shape of $\bs{a}$.
Fonte: Singular Matrix Example 2X2